Cikksorozatunkban bepillantunk a városi alacsonypadlós csuklós autóbuszok anatómiájába, körbejárjuk azokat a kihívásokat, amikkel a konstruktőröknek meg kell küzdeniük egy-egy új karosszéria kifejlesztésekor vagy átalakításakor.
Néha akármennyire nem tűnik úgy, a városi autóbuszok fejlődése folyamatos. Az alacsonypadlós kialakítás lassan két évtizede alapelvárás, a kompromisszumos technológia folyamatos harcot jelent a tágas kialakítás és a gépészet helyigénye között. Mindezek mellett az utasok, megrendelők részéről támasztott követelmények – úgymint modern utastájékoztatás, biztonsági kamera, wifi, stb. – és a szigorodó emissziós és szilárdsági előírások ugyanazt eredményezik, amivel az autóiparnak szűk két évtizeddel ezelőtt kellett először komolyabban szembe néznie: a járművek tömege folyamatosan növekszik.
Az autógyártók esetén azonban másban csúcsosodott ki a probléma: nekik a deciliterekkel, a vezethetőséggel, a szigorodó töréstesztekkel és a gyakran emlegetett NVH-val (zaj, rezgés, nyersesség) kellett megküzdeni. A busziparban azonban, függetlenül attól, hogy ugyanúgy fontos minden komfort- és üzemeltetési költség-beli paraméter, az előírások, a műszakilag és jogszabályilag maximálisan megengedett tengelyterhelések, és a járművek össztömege jelentik a „plafont”, ameddig el lehet menni.
Egy kis statika
Mindannyian tudjuk, hogy amióta Newton feltalálta a gravitációt, minden lefelé esik. Newton viszont nem csak a gravitációt találta fel, hanem harmadik törvényét is. Jelen példánkban csak annyi fontos belőle, hogy ha a buszra erőt fejtünk ki (felszállunk rá, és a súlyunkkal terheljük), és nyugalomban marad, azaz nem süllyed bele az aszfaltba, akkor valahol lennie kell egy ellenerőnek, ami ezt megakadályozza. Ez értelemszerűen a kerekein jelentkezik – a buszt terhelő erők összességének ellenerejét a tengelyterhelések adják ki. Tehát a buszra ható erők vektori összege (a nagyságot és az irányt is figyelembe vevő összege) nulla.
Talán mindannyian emlékszünk gyermekkorunk játszótéri játékára, a mérleghintára. Ha fent voltunk a levegőben, és a másik srác, aki addig a napig a legjobb barátunk volt, leugrott a hintáról, leestünk. A mérleghinta szempontjából azonban ez csak egy szimpla elfordulás volt, ami a súlyunk, mint erő által okozott forgatónyomaték hatására történt meg.
Ha egy testnek egy pontját vagy tengelyét ún. statikai csuklóval rögzítjük a tér egy pontjához, azaz az elmozdulást megakadályozzuk, de az elfordulást nem, akkor ténylegesen létre jöhet a forgás. Ennek megakadályozásához vagy további pontokon / tengelyen rögzíteni kell a testet, vagy különböző egyéb erőkkel és nyomatékokkal ki kell egyensúlyozni azt. Minden olyan erő, amelynek hatásvonala kívül esik a merev test rögzítésén, forgató hatást okoz, amit nyomatéknak nevezünk. A nyomaték annál nagyobb, minél nagyobb az erő, ami létrehozza, és az erő hatásvonala minél távolabb van a vizsgált ponttól, ahol létrejön a nyomaték. Az „üzemszerű” mérleghintázás, vagy a klasszikus kétkarú mérleg így működik.
Newton harmadik törvénye merev testek esetében nem csak az erők, hanem a forgatónyomatékok összességére is érvényes: a forgatónyomatékok előjeles (a forgásirányt is figyelembe vevő) összege nyugalomban lévő test esetén nulla.
Bizonyára többen is kerültünk már olyan helyzetbe, hogy amikor leültünk a sörpad szélére, és a többiek felálltak, a sörpad hirtelen felemelkedett, mint egy mérleghinta. Ilyenkor a súlyunk a sörpad két alátámasztása által közrefogott területen kívül esik, és a sörpad hozzánk közelebbi lábán forgatónyomaték keletkezik. Amennyiben a forgatónyomaték a sörpad távolabbi lábán nagyobb felfelé mutató erőt generál, mint a sörpad saját súlya által generált erő, akkor a sörpad megbillen, és ha nem vagyunk elég gyorsak, esés lehet a vége. Egy busz persze nem fog attól két kerékre állni, hogy a hátsó ajtón szállunk fel, de a modern kipufogógáz-utánkezelő berendezésekkel súlyosbított dízelmotor hasonló hatása már jelentős.
Az álló busz ugye nem megy sehová, nem is forog, tehát nyugalomban van. Ilyenkor fel lehet rá írni a Newton harmadik törvényéből következő egyenleteket: a busz, és adott esetben a teljes rakomány súlya lefelé mutató erőként jelentkezik, és ezek összességével megegyező felfelé mutató erő jelentkezik a tengelyeken. A tengelyek egyben tekinthetők statikai csuklónak is: rögzítik a buszt, de elfordulását (két kerékre állását) nem akadályozzák meg. Így a tengelyek – bár erőt tudnak „közvetíteni” a busz felé, nyomatékot nem. Így olyan egyenletek is felírhatók, amelyeknél az az alapvetés, hogy a tengelyeken nyomaték nem jelentkezik. Erősen leegyszerűsítve ez azt jelenti, hogy az összes, a buszra ható erő – beleértve a busz saját súlyát, és a többi tengely terhelését – vizsgált tengelyre származtatott nyomatéka nulla. Ebből az egyenletrendszerből elméletileg, ha az összes komponens pontos pozícióját és tömegét ismerjük, meg lehet mondani a busz önsúlyát, és tengelyterheléseit.
Klasszikus statika példafeladat a kéttámaszú síkbeli tartó, amire könnyen leképezhető a fenti példabeli sörpad, vagy egy kéttengelyes szóló autóbusz. A csuklósok már egy kicsit bonyolultabb, háromtámaszú csuklós tartónak felelnek meg, de ez még mindig egy egyszerű feladat. A csuklót különösen fontos kihangsúlyozni, hiszen az első és a hátsó, merev kocsirész itt egymáshoz képest elfordulhat, ami nyugalmi helyzetben annyit jelent, hogy nyomatékot nem tudnak egymásnak átadni, csak erőt – így erre a pontra is felírható a nyomatéki egyenlet.
De mi az a nyomatéki egyenlet?
Newton harmadik törvényéből következik, hogy ha egy test nyugalomban van, akkor a rá ható erők és nyomatékok vektori összege – azaz együttes hatása a nagyságot és az irányt is figyelembe véve – nulla.
Ha kiválasztunk egy pontot, amely körül a test szabadon tud forogni, de az egyenes vonalú elmozdulás nem lehetséges – például egy statikai csuklót, vagy egy tengelyt – törvényszerű, hogy az ott ható nyomatékok vektori összege nulla lesz. Egyenes hatásvonalú erő viszont kifejthető a statikai csuklón keresztül.
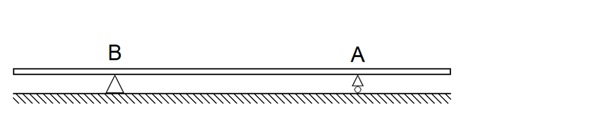
Tekintsük úgy az I. sz. síkbeli tartót, mint egy szóló autóbuszt. Az egyszerűség kedvéért legyen az első túlnyúlás 2,5 m, az A-B távolság 6 m, a hátsó túlnyúlás 3,5 m. A példa kedvéért mondjuk azt, hogy a csupasz vázszerkezet egyenletesen, méterenként 500 kg (12 m esetén 6000 kg) tömegű.
Az ebből származtatott tengelyterheléseket ki tudjuk úgy számolni, mintha a vázszerkezet tömegközéppontjában működne egyedül 6000 kg erő. Ez a középpont az A tengelytől 3,5 méterre van, tehát az A tengelyre származtatott forgató hatása:
• MA = 3,5 m × 6000 kg = 21000 kgm
Ahhoz, hogy a tartónk ne forogjon, a B tengelynek is kell az A tengelyre forgató hatást gyakorolnia, méghozzá ugyanennyit. A B tengely 6 m távolságra van, így a terhelés a forgató hatásból visszaszámítva:
• FB = 21000 kgm / 6 m = 3500 kg
Azt is tudjuk, hogy a szerkezet 6000 kg tömegű, tehát a két tengely terhelése összesen 6000 kg. Ebből következően:
• FA = 6000 kg – 3500 kg = 2500 kg.
Az A tengely terhelése tehát 2500 kg, a B tengelyé pedig 3500 kg.
Ehhez jönnek a hajtáslánc elemei, külső-belső burkolatok, üvegek, egyéb felszerelések, sőt, a tengelyek saját tömege is jelentős. Egy mai szóló autóbusz menetkész tömege 11 tonna alatt már fantasztikusan jónak mondható.
Nézzünk végig egy egyszerű csuklós autóbuszt is a II. Sz. Tartónak megfelelően, hasonló alapadatokkal. Legyen:
az első túlnyúlás 2,5 m,
az A-B tengelytáv 6 m,
a B-csukló táv 1,5 m,
a csukló-C táv 4,5 m,
a hátsó túlnyúlás pedig 3,5 m.
A busz 18 m hosszú, a vázszerkezet teljes tömege így 9000 kg lesz.
A hátsó rész teljes hossza 8 m, ami a C tengelyen és a csuklón nyugvó síkbeli tartónak felel meg. A vázszerkezet 8 m × 500 kg = 4000 kg, tömegközéppontja a C tengelytől 0,5 méterre, a csuklótól 4 méterre van. A csuklóra számolt forgatónyomaték:
• MCS = 4 m × 4000 kg = 16000 kgm
Mivel a busz továbbra sem forog, a C tengely is nyomatékot fejt ki a csuklóra, amintek nagysága megegyezik az Mcs-vel. A C tengely terhelése a fenti analógia alapján:
• FC = 16000 kgm / 4 ,5 m = 3556 kg
De a hátsó rész teljes tömege 4000 kg, ezért a csuklóra is adódik terhelés:
• FCS = 4000 kg - 3556 kg = 444 kg.
A további számítások miatt fontos megjegyezni, hogy ez lefelé terhel.
Az első kocsirészt először is a szóló autóbuszhoz hasonlóan kiszámoljuk. A teljes tömeg 10 × 500 = 5000 kg. A tömegközéppont az A tengelytől 2,5 méterre, a B tengelytől 3,5 méterre helyezkedik el, az A tengelyre származtatott forgatónyomaték:
• MA = 2,5 m × 5000 kg = 12500 kgm
A B tengely A tengelyre kifejtett forgató hatásából származtatott terhelése:
• FB= 12500 kgm / 6 m = 2083 kg
Az A tengely terhelése így:
• FA = 5000 kg – 2083 kg = 2917 kg
Most terheljük rá erre a csuklót, azaz akasszuk össze a két felét a járműnek. Emlékezzünk, a csukló lefelé terhel, tehát a B tengelyt lenyomja, míg az A tengelyt mérleghinta-szerűen megemeli. Fel is tudjuk írni az A tengelyre gyakorolt hatását úgy, hogy elképzeljük a mérleghintát, aminek az egyik felén az A tengely ül, a másik felén csukló, a mérleghinta tengelye pedig a B tengely. Az A tengelyre gyakorolt hatás fordítottan arányos azzal, ahogy az A tengely B tengelytől mért távolsága aránylik a terhelés B tengelytől mért távolságával. Így az eredetileg 2917 kg terhelésű A tengely terhelése a következőképpen alakul:
• FA = 2917 kg - (444 kg × (1,5 m / 6 m)) = 2806 kg
A B tengelyt pedig számítsuk ki az első kocsirészt terhelő erők előjeles összegéből.
• FB = 5000 kg + 444 kg - 2806 kg = 2638 kg
Így az A tengelyen 2806 kg, a B tengelyen 2638 kg, a C tengelyen 3556 kg adódott. 2806 + 2638 + 3556 = 9000 kg. A csukló pedig lefelé van terhelve, 444 kilogrammal.
A busz üresen…
Az autóbuszok – önhordó, vagy alvázas konstrukció esetén is – üres tömegének elég jelentős részét adja a vázszerkezet. Ez – könnyen belátható módon – a tengelyek elhelyezésétől, és a vázszerkezet kialakításától függően többé-kevésbé az összes tengelyt egyenletesen terheli meg. Azonban a busz felöltöztetésekor már rögtön szembe találjuk magunkat egy nagyon jelentős tétellel: a motor, váltó, és az összes kiegészítőjük (hűtőrendszer, kipufogó-rendszer, akkumulátorok, elektronikák, üzemanyag-tartályok stb.) együttes tömege könnyedén meghaladja egy felső-közép kategóriás személyautó tömegét.
Súly? Tömeg? Nyomaték?
Bár a hétköznapokban a két fogalmat gyakran egymás szinonimájaként használjuk, a gyakorlatban azért mást jelentenek.
A tömeg egy test tehetetlenségét fejezi ki, ami azt mutatja meg, hogy mennyi erőt kell kifejteni a test mozgásállapotának megváltoztatásához. Ez a mennyiség minden körülmények között állandó, a Földön, az űrben, a liftben, mindenhol. Effektív módon azt fejezi ki, hogy összességében mennyi elemi részecskéből (proton, neutron, elektron, melyek tömege ismert) áll össze egy test. Ennek a mértékegysége a kilogramm.
A súly ellenben definíció szerint az az erő, amivel a test nyomja az alátámasztását vagy húzza a felfüggesztését. Ennek megfelelően mértékegysége, mint minden erőnek, Newton. Nyugalomban egy 1 kg tömegű test súlya a 45° földrajzi szélességen, tengerszinten 9,80665 Newton.
A forgatónyomaték az erő által generált forgató hatás mértékegysége. 1 m erőkarral (az erő hatásvonala és a tengely közötti legkisebb távolság) 1 N erő 1 Nm (Newtonméter) forgató hatást idéz elő.
Vájtfülűek észrevehetik, hogy a számításokban a tömeget és a súlyt mértékegység tekintetében is ekvivalensként kezeljük. Ez természetesen nem pontos, de tekintve, hogy nyugalomban lévő rendszerről beszélünk, a két mértékenység közötti átváltás mindkét irányban egyértelmű. Amikor tehát azt mondjuk, hogy 1000 kg "erő" a terhelés, az annyit jelent, hogy annyi N erő a terhelés, amennyi egy 1000 kg tömegű test súlya. Ugyanúgy, a 100 kgm forgatónyomaték annyi forgatónyomaték, amennyit egy 100 kg tömegű test súlya 1 m erőkarral működtetni képes a tengelyen.
Ennek megfelelően egy kicsit sem mindegy, hogyan helyezzük el őket a vázszerkezetben, illetve hogy hogyan rendezgetjük alatta az alátámasztásokat, a tengelyeket. Könnyen belátható, hogy a szóló autóbuszon a túlnyúlásokba (azaz az A tengely elé, vagy a B tengely mögé) tett tömegek a hozzájuk közelebbi tengely terhelését növelik, a távolabbi tengelyét csökkentik. Mivel az erők összegének továbbra is nullának kell lennie, ezért a két tengelyre ható erő előjeles összege megegyezik a tömeg súlyával. Ebből következően a túlnyúlásokba tett tömegek saját súlyuknál nagyobb erővel fogják terhelni a hozzájuk közelebbi tengelyt.
Terheljük meg a vázunkat
A fenti szóló autóbuszra vonatkozó példánál maradva, az üres, 6000 kg-os vázszerkezetbe beemeljük a motor-váltó kombinációt. Legyen a tömege 1500 kg, és a B tengelytől 2 méterre hátrafelé helyezzük el a tömegközéppontot.
Képzeljük el a mérleghintát, aminek az egyik felén az A tengely ül, a másik felén a hajtáslánc, a mérleghinta tengelye pedig a B tengely. Az eredetileg 2500 kg terhelésű A tengely terhelése a következőképpen alakul:
• FA = 2500 kg - (1500 kg × (2 m / 6 m)) = 2000 kg
A teljes buszunk tömege viszont már 7500 kg, így a B tengely terhelése a következőképpen változik:
• FB = 7500 kg – 2000 kg = 5500 kg
Az A tengely új terhelése 2000 kg, a B tengelyé pedig 5500 kg lesz. Láthatjuk tehát, hogy a szerencsés pozicionálásnak köszönhetően 2000 kilogrammal sikerült növelni a B tengely terhelését egy mindössze 1500 kg-os tömeg segítségével.
A csuklós autóbuszon bonyolultabb a helyzet. Egy tolócsuklós autóbusz motorjának és váltójának súlya a C tengely mögé helyezve lefelé mutató erőt fejt ki a hátsó merev részre, amit mérleghinta-szerűen akarja elfordítani a C tengely körül. Ebben csak a csuklónál ható, szintén lefelé mutató ellenerő akadályozza meg. A nyomatéki egyenletet az A tengelyre felírva mindjárt látszik, hogy a csuklóban ébredő erő a B tengelyt nem terheli, hanem ,,felfelé" húzza. Ha tehát nincs elég terhelés a B tengelyen a vázszerkezet és az egyéb berendezések által, a terhelése akár túlságosan is lecsökkenhet, miközben a C és az A tengelyé erősen megnövekszik.
A motor hatását ellensúlyozza az akkumulátor és az üzemanyagtartály, nyilakkal jelölve. Na és persze a csuklószerkezet is.
A buszgyártók valós problémája a tolócsuklós autóbuszok esetén, hogy a B tengely terhelése túl alacsony. Ennek kiküszöbölésére szándékosan a B tengely közvetlen közelébe, vagy a B és a C tengely közé helyezik a többlet-terheléseket (pl.: akkumulátor, klímaberendezés tetőegységei, üzemanyagtartály).
De miért lesz alacsony a B tengely terhelése?
Fenti példánkat folytatva, tegyük be a csuklós járműbe is a hajtásláncot, ami ezúttal legyen 2000 kg. A pozíció ugyanott van, a C tengelytől hátrafelé 2 méter távolságban.
A csuklóra adódó teljes hatás így a következőképpen változik:
• Fcs = 444 kg - (2000 kg × (2 m / 4,5 m) = -445 kg
Azaz a csukló ezúttal felfelé van terhelve 445 kg-mal.
A C tengely új terhelését a hátsó kocsirészre ható erők előjeles összegéből megkapjuk:
• Fc = 4000 kg + 2000 kg + 445 kg = 6445 kg.
Ugyanúgy, mint a szóló autóbusz esetében, itt is az eredetileg 3556 kg-os tengely terhelését majd' három tonnával növeltük meg egy jól pozícionált 2 tonnás tömeg segítségével.
Nade nézzük tovább az első kocsirészt. Összeakasztás nélkül a tengelyek terhelése FA = 2917 kg; FB = 2083 kg. A fenti számítás második felét pedig csináljuk végig úgy, hogy ezúttal a csukló terhelésének iránya megváltozott, és ezzel az előjelek is változnak:
• FA= 2917 kg + (445 kg × (1,5 m / 6 m)) = 3028 kg
Az első kocsirészt terhelő erők előjeles összegéből a B tengely:
• FB = 5000 kg - 445 kg - 3028 kg = 1527 kg
A teljes tömegnek ezúttal 11000 kg-nak kellene lennie, az A tengely a fentiek alapján 3028 kg, a B tengely 1527 kg, a C tengely pedig 6445 kg, 3028 + 1527 + 6445 = 11000.
Látszik, hogy a B tengely terhelése csaknem fele az A tengelyének, és a C tengely terhelésének kevesebb, mint a negyede. Ez járműdinamikailag enyhén szólva sem kívánatos. Ha a jármű arányait nem megfelelően választjuk meg, a probléma még inkább kicsúcsosodik.
Egy kis számolgatással látható az is, hogy a B tengely terhelésére jótékony hatással van az, hogyha a motor közel esik a C tengelyhez, és a C és B tengelyek is messze esnek a csuklótól. Ezek viszont további problémákat vetnek fel: az optimális utastér-kialakítás, és a minimális kardánhossz miatt a motor nem rakható akármilyen közel a C tengelyhez, a csuklótól messze lévő C tengely hosszabb hátsó részt és nagyobb tengelyterhelést jelent, a csuklótól messze lévő B tengely miatt pedig a busz becsuklásra hajlamosabb lesz (hogy miért, az a cikksorozat következő részéből kiderül).
Mi történik, ha ugyanannál a busznál lecsökkentjük a C tengely és a csukló távolságát és a csuklószerkezetet könnyebbre cseréljük? A B tengely terhelése extrém módon lecsökkenhet. Azt majd meglátjuk, hogy ez miért baj.
A húzócsuklós autóbuszok a közelmúltig valós alternatívát jelentettek, azonban az utastér-kialakítás tekintetében egyértelműen rosszabbak, mint egy farmotoros elrendezésű jármű. Emellett a motor segédberendezéseinek méret- és tömegbeli növekedésével egyre nagyobb problémát jelentett a motor elhelyezése a két tengely között. Látni fogjuk, hogy a húzócsuklósok helyzete utasokkal terhelve sem javul túlságosan.
…és tele
Ahogy az ismert példában a professzor úr befőttes üvege, úgy az autóbusz is többféleképpen lehet tele. A triviális szempontokon túl, hogy a busz egyensúlya ne boruljon fel, a tengelyek ne emelkedjenek a levegőbe, illetve hogy a vázszerkezet méretezése elviselje a felmerülő terheléseket, a legfontosabb további teendő a törvényi megfelelőség biztosítása.
Az autóbuszok típusvizsgálata során Európában az ENSZ-EGB 107. sz. előírását veszik alapul, aminek idevágó, 3.2.3.2.1. sz. passzusa, közforgalmú városi buszokra értelmezve röviden annyit jelent, hogy ülésenként egy 68 kg-os utas foglal helyet, és az állóhelyen egyenletesen oszlanak el további 68 kg-os utasok, de egy utas minimum 0,125 m2 helyet (8 fő/m2) foglal el. Ez akkora embertömeg, mintha egy 200-as Ikarus lépcsőjén 4 fő állna, vagy mintha egy átlagos telefonfülkében 5 fő zsúfolódna össze, csak a telefonfülke még mozog is, és a belső ember kétpercenként ki akar jutni.
A jogszabály maximális utasonkénti területet, vagy fordítva, minimális utassűrűséget nem határoz meg. Tehát a vizsgálóintézet és a gyártó józan belátása alapján a típusbizonyítványba, és az az alapján kiállított forgalmi engedélybe, a maximális szállítható utasszám rubrikába olyan értékek is bekerülhetnek, amelyek a maximális utassűrűségnél kisebb utassűrűséget feltételeznek.
A magyar hatályos jogszabály, a közúti járművek forgalomba helyezéséről szóló 6/1990 (IV. 12.) KöHÉM rendelet többé-kevésbé konform az ENSZ-EGB előírásokkal, ami a szállítható személyek számának meghatározásakor minden négyzetméterre 8 személyt ír elő a 20. § (4) bekezdésében, azonban nyitva hagy egy kiskaput.
De miért is fontos ez a kiskapu? Hiszen a gyártó – már csak marketing-szempontból is – nem abban érdekelt, hogy minél nagyobb befogadóképességű járművet gyártson? És ez alapján nem az a legkedvezőbb megoldás, ha a legsűrűbb, 8 fő/m2 értékkel számol? De igen, csakhogy itt jön a képbe a másik plafon: a tengelyterhelés- és tömegelőírásoknak való megfelelés kérdése.
Szabál, szabál…
A jogalkotó – nem jókedvéből, hanem az általa fenntartott infrastruktúrát megvédendő, a jelenlegi helyzetnél is gyorsabb nyomvályúsodást és kátyúsodást, nem adj’ isten aszfalt-beszakadást elkerülendő – maximalizálta a tengelyterheléseket.
A típusvizsgálat során, az ENSZ-EGB előírásban leírtak szerint, az üres jármű hiteles mérés során lemért tengelyterheléseiből, az ülések pozíciójából és az állóhely geometriájából, az egész állóhely-felületet egy egyenletesen megoszló terhelésként értelmezve, a fent megismert nyomatéki egyenletek segítségével kiszámolják az elméleti megengedett maximális tengelyterhelést és az össztömeget.
Hogyan is történik ez?
Vegyük a példa-beli szóló autóbuszunkat, ezúttal már menetkészen. Az A tengely terhelése legyen 4000 kg, a B tengelyé pedig 7000 kg. Osszuk fel az állóhely-területeket ismert méretű és súlypontú síkidomokra, valahogy úgy, ahogy az ábrán látható:
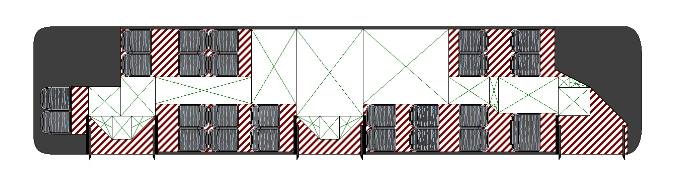
Osszuk fel a buszt három szekcióra, első túlnyúlás, két tengely közötti szekció, és hátsó túlnyúlás.
Egy ismert terhelés hatásának kiszámításához fel tudjuk írni a következő egyenleteket:
Az első túlnyúlásban:
ΔFB = -(m × (dA/dAB))
ΔFA = m + ABS(ΔFB)
A hátsó túlnyúlásban:
ΔFA = -(m × (dB/dAB))
ΔFB = m + ABS(ΔFA)
A két tengely között pedig:
ΔFA = m × (dB/dAB)
ΔFB = m × (dA/dAB)
Ahol dA, illetve dB a terhelés távolsága az A, illetve B tengelytől, dAB a tengelytáv, m pedig a terhelés tömege. Az ülések pozícióinak, a síkidomok területének és súlypontjának ismeretében végig számolható az egész jármű.
A példa kedvéért számoljuk ki a 75 kg-os sofőr hatását, aki 1,5 méterrel ül az első tengely előtt:
ΔFB = -(80 × (1,5/6) = -20; FB= 6980 kg
ΔFA= 80 + 20 = 100; FA = 4100 kg
Szálljon fel még egy babakocsis anyuka is pont a két tengely közé középre, akinek a tömege a gyerkőccel, babakocsival együtt 60 kg:
ΔFA = 60 × (3/6) = 30; FA= 4130 kg
ΔFB = 60 × (3/6) = 30; FB = 7010 kg
És szálljon fel a hátsó ajtón egy négy fős társaság, aki összesen 300 kg, és a B tengelytől hátrafelé 0,5 méterre állnak meg:
ΔFA = -(300 × (0,5/6)) = -25; FA = 4105 kg
ΔFB = 300 + 25 = 325; FB = 7335 kg.
Összesen 80 + 60 + 300 = 440 kg terhelést tettünk fel a buszra, a két tengely terhelése pedig 4105 + 7335 = 11440 kilogrammra adódott.
Aki kicsit jártas az Excel világában, ebből könnyen tud csinálni egy táblázatot, amelybe a terhelések mértékét és pozícióját csak be kell írogatni, és automatikusan számítódnak a tengelyterhelések.
A vizsgálóintézetben nem csak rajzból dolgoznak, hanem a valóságban is lemérik az ülések és a síkidomok pozícióját, területét.
A típusvizsgálat során az európai Tanács 96/53/EK irányelvének 3. pontjára tekintettel vizsgálják a legnagyobb megengedett tengelyterhelést, ami a városi buszok tekintetében nem hajtott tengelynél a 10 tonnát, hajtott tengelynél a 11,5 tonnát nem haladhatja meg. A fentebb már említett 6/1990 KöHÉM rendelet ezzel az előírással megegyező elvárásokat fogalmaz meg a 7. §-ban. A tanácsi irányelv 2. pontja szerint a kéttengelyes, városi szóló autóbusz össztömege mindezek mellett sem haladhatja meg a 18 tonnát, míg a városi csuklós, háromtengelyes autóbuszok legfeljebb 28 tonna össztömegűek lehetnek. A KöHÉM rendelet 6. §. a kéttengelyes szóló autóbuszokkal szemben megengedőbb, a 20 tonnás járművek is megfelelnek.
A C tengely és a csukló távolságának változtatása esetén a tengelyterhelések alakulása, ceteris paribus
További korlátot jelent a futóművek műszakilag megengedett terhelhetősége, ami például a gyártók körében mellső tengelyként népszerű ZF RL 82 EC független felfüggesztés esetében 8,2 tonna, vagy a ZF RL 75 A merevtengely esetében 7,5 tonna. A szintén népszerű ZF AV 133 hajtott tengely technikailag akár 13 tonnás terhelést is kibír.
A gumiabroncsok teherbírása szintén véges, a gyakori, 275/70 R22,5 méretű, prémium kategóriájú Continental Conti Urban gumiabroncs szimpla abroncsozással, maximális 900 kPa nyomáson tengelyenként 7,1 tonnát, dupla abroncsos konfigurációban 12,6 tonnát vihet a hátán.
Itt kell visszautalnunk a húzócsuklós autóbuszokra: az első kocsirész jelentősen magasabb saját tömege miatt az nem terhelhető túlságosan sok utassal – igaz, a motorsátor „hatékonyan” csökkenti az utasok rendelkezésére álló területet – a hátsó résszel pedig hamar elérhetjük a tengelyterhelés műszaki korlátait, így hiába a kedvező tengelyterhelés-megoszlás, így sem egyszerű nagy befogadóképességű autóbuszt csinálni.
A modern, EURO 6 emissziós normáknak és az ENSZ-EGB 66. sz. előírásban támasztott tetőszilárdsági követelményeknek megfelelő, szellős utastérrel rendelkező városi autóbusz esetén borítékolható, hogy a maximális utassűrűség nem érhető el az állóhely-területen. Így viszont a szállítható személyek számát kell csökkenteni, de tekintve a 8 fő/m2 elvárás abszurditására és megvalósíthatatlanságára, ez önmagában talán nem is baj.
Az is nehezen képzelhető el, hogy egy jármű csak úgy „megbukik” a típusvizsgálaton, mint egyszeri hallgató a statika vizsgán, mert a gyártó 6 fő/m2 értékkel adta meg az intézethez benyújtott adatlapon a tömegszámítási paramétereket, míg a jogszabályilag meghatározott maximális tengelyterhelés már 5,9 fő/m2 értéken jelentkezik.
A típusvizsgálat során ugyanis a vizsgálóintézet a szabályok adta lehetőségeken belül interaktív módon kommunikál a gyártóval, és az könnyen előfordul, hogy a vizsgálóintézet jelzi, hogy a benyújtott adatlapon szereplő tömegértékekhez képest ő pár százalékkal különböző, esetleg a jogszabályoknak már nem megfelelő eredményre jutott, és felkéri a gyártót a szolgáltatott adatok felülvizsgálatára, vagy adott esetben a gyártmány módosítására.
Na jó, de mennyi az annyi?
A legtöbb esetben a típusbizonyítványokban megengedett álló utas sűrűség 5-6 fő/m2 az alacsonypadlós tolócsuklósok esetén.Például a VT.Transman Mercedes Citaro C2G típusú autóbuszok esetén a 4fő/m2-rel számított állóutas kapacitás 66 fő. 66 fő osztva a 4fő/m2-rel az 16,5-16,74 négyzetméter közötti állóterületnek adódik, mivel az utasok számát minden esetben lefelé, egész számra kell kerekíteni. A busz típusjóváhagyásában erre az üléskiosztásra 100 fő álló utas szerepel, ami 5,9-6 fő/m2 utas-sűrűséget jelent.
A vezető mellé felragasztott matricára felvitt adatok újabban egyeznek a típusjóváhagyásban szereplőkkel.
Nagy állóterekkel ellátott 18 méteres busz (pl. Conecto G Budapesten) hasznos állófelülete 17,4 m2 körülre tehető, ahogy a 18,75 méter hosszú szegedi Ikarus trolinak is pontosan ennyi, különösebben nagy peronok nélkül.
Fontos megjegyezni, hogy a padlófelület számításból a 8 foknál nagyobb lejtésű területeket ki kell zárni.
Mindenképpen meg kell jegyezni azt is, hogy az illetékes hatóság, aki a vizsgálóintézet jegyzőkönyve alapján a típusbizonyítványt kiállítja, vagy a Közösség más országában kiállított típusbizonyítvány befogadásáról dönt, bizonyos esetekben, bizonyos közösségi és nemzeti jogszabályi keretek között, bizonyos előírások alól mentességet adhat. Ebben az esetben viszont a mentességet adó hatóságnak mindenképpen meg kell győződnie arról, hogy a mentesség ellenére, az előírások céljának megfelelő-e a jármű kialakítása, és ezért ő felelősséget vállal. Ebben az esetben nem feltétlenül kell magyar, vagy éppen román-bolgár-horvát mutyira gondolni, Budapesten is közlekedik olyan jármű, amely bizonyos közösségi irányelvek és előírások tekintetében – ha nem is teljes felmentést, de kedvezményt kapott, nem mástól, mint a német közlekedési hatóságtól.
A következő részben elindulunk a busszal és a tömeggel, megnézzük, hogy járműdinamikailag mi történik a csuklós busszal egy jobbra, kis ívben, álló helyzetből történő kikanyarodáskor, és milyen rendszerek dolgoznak azért, hogy a járművezetőinek és utasainak semmi különös ne tűnjön fel ilyen helyzetekben.
A képek forrásai: Daimler, Solaris, ZF
